Декартова (правоъгълна) координатна система

Декартовата (правоъгълна) координатна система е предложена за първи път през 1637 г. от Рене Декарт (1596 – 1650).

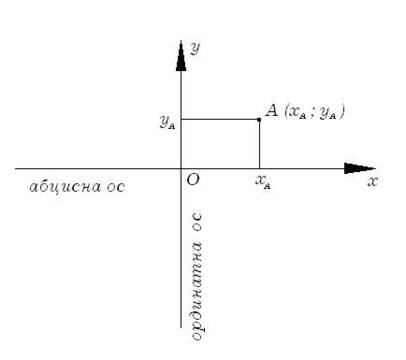
Правоъглната кооординатна система представлява две перпендикулярни числови оси с общо начало – пресечната точка О и избрана една и съща мерна единица върху двете оси. Означаваме Оху или хОу.

Точка О се нарича начало на декартовата координатна система.
Оста Ох е абцисна ос (хоризонтална ос).
Оста Оy е ординатна ос (вертикалана ос).

Мястото на произволна точка А се определя от числата хА и уА, които се наричат координати на точка А и записваме:
А (хА; уА)
хА се нарича абциса на точка А;
уА се нарича ордината на точка А.

Пример:

Точка N (-2; 4) е с абциса –2 и ордина 4;
Точка N1 (2; 4) е с абциса 2 и ордина 4;
Точка М (3; 1) е с абциса 3 и ордина 1;
Точка М1 (3; -1) е с абциса 3 и ордина -1;
Точка А (-3; -2) е с абциса -3 и ордина –2.

Точка А има координати хА = -3 и уА = -2 т.е. тя се определя с наредената двойка числа ( -3; -2). Важно е кое число е първо и кое второ. Абцисата (хА) е първа, ординатата (уА) е втора. Наредената двойка числа ( -2; 4) определят точка N, както ( 2; 4) определят точка N1.

Квадранти на правоъгълната координатна система

Двете оси разделят равнината на четири части наричани квадранти.

За всеки от квадрантите е характерно:
– І квадрант – точките в този квадрант имат (+) абциса и (+) ордината;

– ІІ квадрант – точките в този квадрант имат (-) абциса и (+) ордината;

– ІІІ квадрант – точките в този квадрант имат (-) абциса и (-) ордината;

– ІV квадрант – точките в този квадрант имат (+) абциса и (-) ордината.

Симетрични точки

М и М1 са симетрично разположени спрямо ос Ох – това значи, че двете точки се намират на еднакво разтояние от оста Ох.
N и N1 са симетрични спрямо ос Оy – двете точки се намират на еднакво разтояние от оста Оy.
Точка А и А1 са симетрични спрямо началото О.
Точка B и B1 са симетрични спрямо началото О.